Pretty Endpoints

MOE has a C++-based optimizer that is exposed via a Python-based REST API server. The API comes with an interesting feature, pretty endpoints. If there’s an endpoint, /foo, then you can visit /foo/pretty in your web browser and see an interactive example. The page has example JSON that you can submit, edit, and resubmit.

It’s pretty cool, but it left me wishing for a more traditional API reference when I wanted to go from a one-dimensional search to a two-dimensional search.

The REST client that comes with MOE is pretty well documented, so I ran another copy of the MOE container.

sudo docker run -it -u root -v ~/experimental/moe-user:/mnt --entrypoint=/bin/bash yelpmoe/latest

In there, I hacked the Python REST client to log its JSON messages to a file in /tmp and examined that when running the example 2D search that comes with MOE. Then I saw the format I had to use.

{"domain_info": {"dim": 2, "domain_bounds": [{"max": 5.0, "min": -5.0}, {"max": 5.0, "min": -5.0}]}, "gp_historical_info": {"points_sampled": []}, "num_to_sample": 1}

I already guessed that you have to say that "dim" is 2, but I noticed that you also have to provide a min and max pair for each dimension.

Something to Optimize

I wanted to have a function with local minima and a global minimum, so I added a cosine to a parabola.

library(ggplot2)

true.fn <- function(x) {
    d <- sqrt(sum(x^2))
    y1 <- d^2 / 100
    y2 <- cos(d) / -4
    (y1 + y2)
}

grid <- function(x, y) {
    m <- matrix(nrow=length(x) * length(y), ncol=2)
    rowi <- 1
    for (i in 1:length(x)) {
        for (j in 1:length(y)) {
            m[rowi,] <- c(x[i], y[j])
            rowi <- rowi + 1
        }
    }
    m
}

domain <- function() {
    x <- seq(-20, 20, by=0.5)
    y <- x
    grid(x, y)
}

mk.data <- function() {
    m <- domain()
    m <- cbind(m, apply(m, 1, true.fn))
    colnames(m) <- c("x", "y", "z")
    data.frame(m)
}

show <- function() {
    ggplot(mk.data(), aes(x=x, y=y, z=z)) + geom_contour()
}

show.x <- function() {
    d <- mk.data()
    ggplot(d[d$y == 0,], aes(x=x, y=z)) + geom_line()
}

show.x()

It’s easier to see in one dimension, but it’s a two-dimensional function.

show()

Any Client

Now I wanted to try out MOE from Python but without using their Python library. It sounds odd, but consider that 1) I might want to use some other language, maybe one that isn’t out yet, and 2) I have been using Python 3 preferentially, and their Python REST client libraries seem more comfortable with Python 2.7.

Here’s the code that uses JSON directly.

#! /usr/bin/env python2.7

from __future__ import print_function

import json
import math
import os
import requests

from addict import Dict
import click
import numpy as np


API = 'http://localhost:6543/gp/next_points/epi'


def true_fn(point):
    d = np.sqrt(
        pow(np.array(point, dtype=np.float32), 2).sum())
    y1 = pow(d, 2) / 100
    y2 = math.cos(d) / -4
    return y1 + y2


@click.option(
    '--max-iter', default=3
)
@click.option(
    '--verbose', default=False, is_flag=True
)
@click.command()
def main(max_iter, verbose):
    exp = Dict({
        "domain_info": {
            "dim": 2,
            "domain_bounds": [
                {"max": 20.0, "min": -20.0},
                {"max": 20.0, "min": -20.0},
            ]
        },
        "gp_historical_info": {
            "points_sampled": [],
        },
        "num_to_sample": 1,
    })
    best_point = None
    best_val = None
    for i in range(max_iter):
        if verbose:
            print(json.dumps(exp))
        r = requests.post(API, data=json.dumps(exp))
        if verbose:
            print(r.text)
        nextpt = [float(i)
                  for i in json.loads(
                          r.text)['points_to_sample'][0]]
        val = true_fn(nextpt)

        s = ''
        if best_point is None or val < best_val:
            best_point = nextpt
            best_val = val
            s = '  ... A WORLD RECORD!!!'

        print('f({}) = {}{}'.format(nextpt, val, s))

        exp.gp_historical_info.points_sampled.append({
            "value_var": 0.01,
            "value": val,
            "point": nextpt,
        })


if __name__ == '__main__':
    main()

Yeah, yeah. I know—I used Python 2.7 right after I said I prefer Python 3. Call me a hypocrite. The point is that anything can print JSON.

The output looks something like this:

ecashin@montgomery:~/experimental/moe-user$ ./useapi_2d.py --max-iter 20
f([-19.4211329705, 16.1817903783]) = 6.14297928492  ... A WORLD RECORD!!!
f([-10.1536519406, -14.1447713031]) = 2.99854690833  ... A WORLD RECORD!!!
f([-4.08891069113, -7.77026636892]) = 0.970837639895  ... A WORLD RECORD!!!
f([7.89655712959, -16.2536583322]) = 3.0875048342
f([0.557183035696, 0.089724831252]) = -0.208047592448  ... A WORLD RECORD!!!
f([-1.17069715023, 0.183623456291]) = -0.0800293795817
f([-0.0212410306582, -1.56499600174]) = 0.023082594082
f([0.225741656362, 1.78274736612]) = 0.0883571884112
f([2.30178362082, 0.260580016253]) = 0.223280866099
f([-3.75559521582, -1.26936274927]) = 0.327215201349
f([1.07484307288, 13.7023252526]) = 1.79340747812
f([12.1463972019, 12.6231103474]) = 3.0095546387
f([19.2194897527, 3.76973996397]) = 3.65073229955
f([18.9615251931, -12.2498296432]) = 5.30466432742
f([-13.0612450007, 5.59698062173]) = 2.03739960908
f([-8.39848964969, 14.0978753142]) = 2.88374592401
f([-18.7357357443, -11.5192903881]) = 5.08721754187
f([17.4818277491, 19.9567035878]) = 6.99587824901
f([-2.03383613494, -18.024251427]) = 3.1006606068
f([7.36148447862, -7.24269082653]) = 1.2214368028
ecashin@montgomery:~/experimental/moe-user$ 

If I increase the number of iterations, I can see that MOE jumps around a lot in the little box from \((-20, -20)\) to \((20, 20)\). It quickly finds some pretty good points but then spends a lot of time trying different combinations of coordinates.

If I change the output to CSV, I can plot the search by using gganimate for the first time ever.

library(dplyr)
## 
## Attaching package: 'dplyr'
## The following objects are masked from 'package:stats':
## 
##     filter, lag
## The following objects are masked from 'package:base':
## 
##     intersect, setdiff, setequal, union
library(ggplot2)
library(gganimate)

d <- read.csv('search.csv', header=TRUE)
p <- ggplot(d, aes(x=x1, y=x2, frame=iter, label=iter, cumulative=TRUE)) +
  geom_text()

Then I call gganimate() to get the gif below.

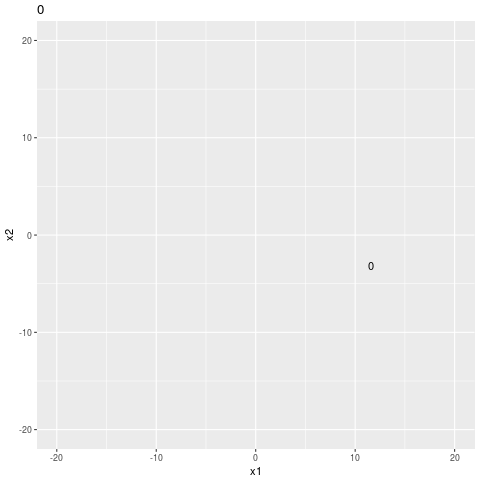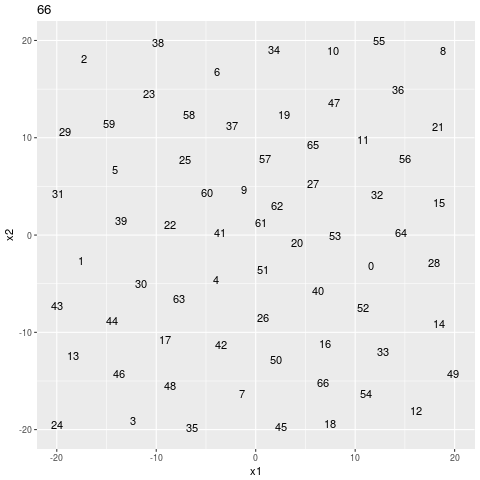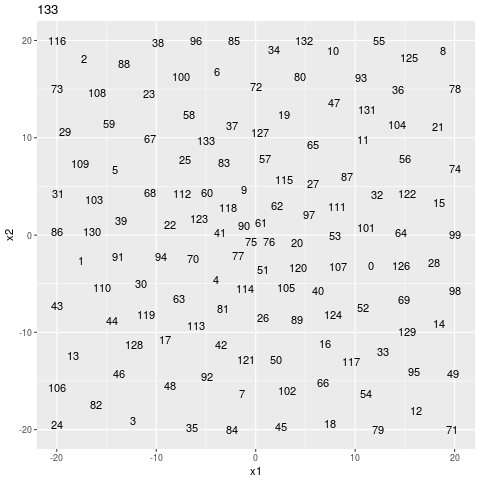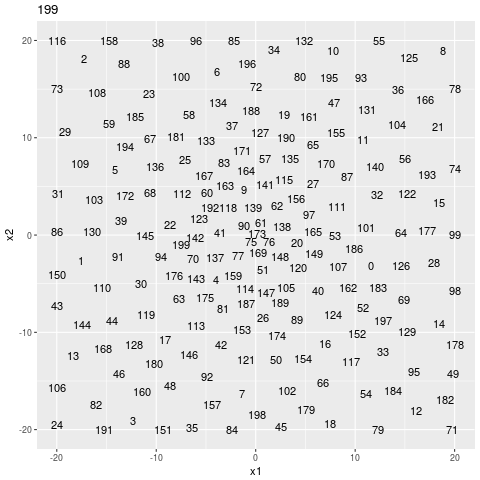
search sequence

I think that it has to explore all the gaps because I intentionally made the search hard.

Easier Optimization

If I modify the true function to remove the bumps, leaving only a parabola, the optimizer has an easier job to do.

def true_fn(point):
    d = np.sqrt(
        pow(np.array(point, dtype=np.float32), 2).sum())
    y1 = pow(d, 2) / 100
    # y2 = math.cos(d) / -4
    return y1 #  + y2

Running the optimizer one hundred times, I get search-easy.csv, and I recreate the gganimate plot below.

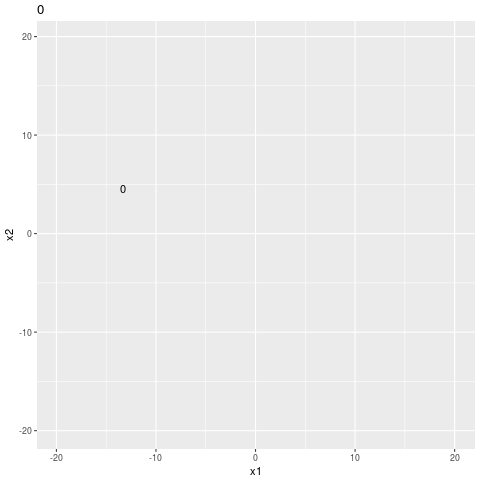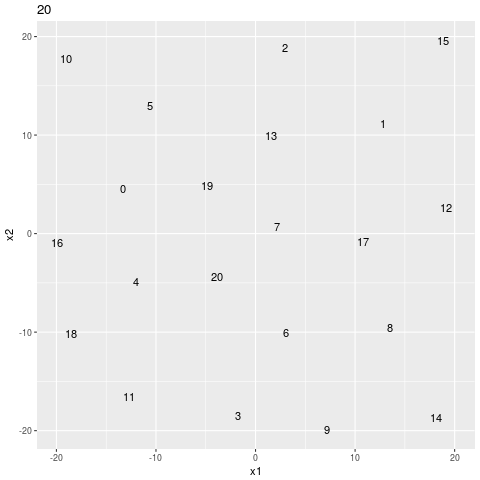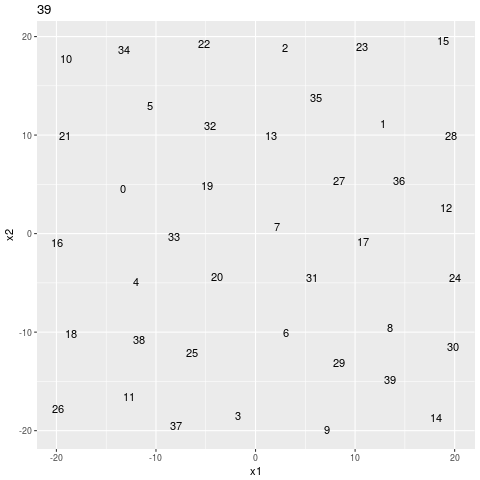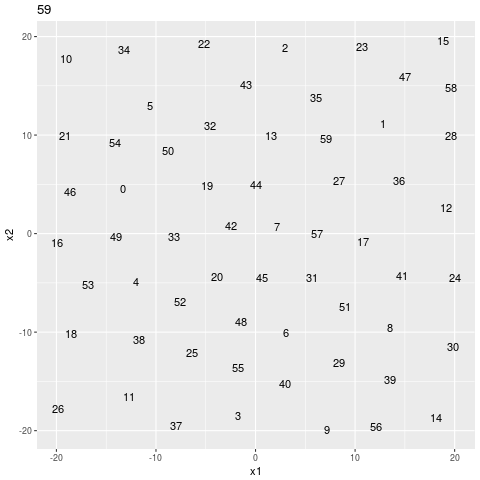
easier search sequence

It looks like it still doesn’t trust the easy answer. If it was just descending the gradient it would just shoot right on down the hill to the origin, but it’s skeptical, like it doesn’t want to miss a little unexpected minimum in a less well expored part of the manifold.

Scaling Up

The whole point is that the function is expensive to evaluate, so it isn’t that big a deal if there’s some latency going through REST. Still, I want to get some idea of how many dimensions I can expect to use with a “reasonable” query time, and how many points I can add before things get unwieldy.

I go to 100 points for each of 4, 8, 16, \(...\), 512 dimensions. For each iteration, a point is added to the historical information, and the query time in milliseconds is reporting.

The plot below is surprising. Four dimensions is very slow (as was two); however, higher numbers of dimensions enjoy quicker queries. Maybe MOE switches strategies for higher numbers of dimensions.

d <- read.csv("scale-up.csv", header=TRUE) %>% mutate(ndim=factor(ndim))
ggplot(d, aes(x=iter, y=query_msecs, color=ndim)) + geom_point()

The final version of the Python script is shown below.

#! /usr/bin/env python2.7

from __future__ import print_function

import json
import math
import os
import requests
import time

from addict import Dict
import click
import numpy as np


API = 'http://localhost:6543/gp/next_points/epi'


def true_fn(point):
    d = np.sqrt(
        pow(np.array(point, dtype=np.float32), 2).sum())
    y1 = pow(d, 2) / 100
    y2 = math.cos(d) / -4
    return y1 + y2


@click.option(
    '--max-iter', default=3
)
@click.option(
    '--verbose', default=False, is_flag=True
)
@click.option(
    '--n-dim', default=2
)
@click.command()
def main(max_iter, verbose, n_dim):
    exp = Dict({
        "domain_info": {
            "dim": n_dim,
            "domain_bounds": []
        },
        "gp_historical_info": {
            "points_sampled": [],
        },
        "num_to_sample": 1,
    })
    for _ in range(n_dim):
        exp.domain_info.domain_bounds.append(
            {"max": 20.0, "min": -20.0})
    best_point = None
    best_val = None

    print('iter,ndim,query_msecs')

    for iter in range(max_iter):
        if verbose:
            print(json.dumps(exp))
        start = time.time()
        r = requests.post(API, data=json.dumps(exp))
        query_msecs = (time.time() - start) * 1000

        if verbose:
            print(r.text)
        nextpt = [float(i)
                  for i in json.loads(
                          r.text)['points_to_sample'][0]]
        val = true_fn(nextpt)

        if best_point is None or val < best_val:
            best_point = nextpt
            best_val = val

        print('{},{},{}'.format(
            iter,
            n_dim,
            query_msecs))

        exp.gp_historical_info.points_sampled.append({
            "value_var": 0.01,
            "value": val,
            "point": nextpt,
        })


if __name__ == '__main__':
    main()